Logo
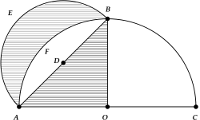
Logoet er relateret til problemet med Hippokrates' måner. Hippokrates arbejdede med at kvadrere cirklen, i den forbindelse betragtede han følgende problem: Tegn to cirkelbuer med fælles korde, samt linjerne som forbinder de to centre med enderne af korden.
Med passer og lineal er det så muligt at konstruere sådanne cirkelbuer således at arealet mellem de to cirkelbuer er lig med arealet afgrænset af radierne?
Hippokrates fandt selv to løsninger, bla. løsningen vist på tegningen (fra Wikipedia).
Ud over de to Hippokrates fandt i antikken, beskrev danske Thomas Clausen to løsninger i 1840. At $\pi$ ikke kunne kvadreres blev bevist i 1882, men vi skal helt op i midten af det 20. århundrede før alle Hippokrates' måner var klassificeret. Nikolai Chebotaryov og Anatoly Dorodnov viste at der kun er fem løsninger som kan konstrueres med passer og lineal.
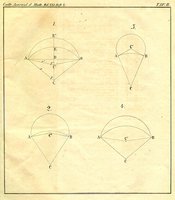
DMFs logo er frit efter en af skitserne fra Thomas Clausens originale artikel. (Bemærk at vinklerne i logoet ikke svarer til den korrekte løsning.) Clausens skitser kan ses i kolonnen til højre.
Thomas Clausen (1801-85) født i Sottrup, læste astronomi ved observatoriet i Altona og blev 1843 leder af observatoriet i Dorpat, det nuværende Tartu i Estland. Clausen er især kendt for en sætning sammen med von Staudt om Bernoullital, formlen for hypergeometriske funktioner: \[ _3F_2 \begin{bmatrix} 2a, 2b, a+b; x \\ 2a+2b , a+b+\tfrac12 \end{bmatrix} = \left( _2F_1 \begin{bmatrix} a,b ; x \\ a+b+\tfrac12 \end{bmatrix}\right)^2 \]
Nogle links
Youtube kanalen Numberphile har også behandlet disse måner, omend fra en lidt anderledes vinkel.